如果想要用程序控制车辆的运行, 需要先建立车辆运动的数学模型. 车辆的运动学模型已经很成熟了, 并且有多种, 可参考: https://zhuanlan.zhihu.com/p/103834150, https://blog.csdn.net/AdamShan/article/details/78696874, https://zhuanlan.zhihu.com/p/130502383 等.

本文介绍最广泛使用的自行车模型, 以及如何生成行车辅助线.

前轮驱动的自行车模型

自行车模型(Bicycle Model)非常简单, 基于如下假设建立:

不考虑车辆在垂直方向(Z轴方向)的运动，即假设车辆的运动是一个二维平面上的运动。
假设车辆左右侧轮胎在任意时刻都拥有相同的转向角度和转速；这样车辆的左右两个轮胎的运动可以合并为一个轮胎来描述。
假设车辆行驶速度变化缓慢，忽略前后轴载荷的转移。
假设车身和悬架系统都是刚性系统。
假设车辆的运动和转向是由前轮驱动(front−wheel−only)的。

因此, 我们把一辆车的运动抽象成只有前后两轮的自行车, 很简单:

以下描述这个自行车模型的运动模型:

其中:

ICR: 车轮的旋转中心
R: 转弯半径
δ: 车轮的转角
L: 轴距(前后车轴的距离)

因为程序控制车辆运动时需要地图, 或者说坐标, 所以我们需要把上述模型放到坐标系中讨论:

其中 θ是车辆相对于坐标系的朝向角. 因为不同的坐标系之间可以相互转换, 因此此处的(X, Y)坐标系可以是车体坐标系, 相机坐标系, 世界坐标系等等, 并不限制.

变量	含义	下一时刻的值	备注
x	车辆坐标: x	x = x + v * cos(θ) * dt	坐标: x
			下一时刻的x = 当前时刻的x + 短时移动距离在X方向的分量
			下一时刻的x = x + v * cos(θ) * dt
y	车辆坐标: y	y = y + v * sin(θ) * dt	坐标: y
			下一时刻的y = 当前时刻的y + 短时移动距离在Y方向的分量
			下一时刻的y = y + v * cos(θ) * dt
θ	车辆朝(航)向角度	θ = θ + v * tan(δ) / L * dt	车头朝向: (假设车辆慢速, 转向中心不变, 则后轮角速度 = 前轮角速度 = 车辆朝向角速度)
			下一时刻的车头朝向 = 当前时刻的车头朝向 + 前轮角速度 * 时间间隔
			其中:
			(1) 后轮角速度 = V / R
			(2) 而tan(δ) = L / R
			(3) 联立(1)(2)可得: 后轮角速度 = V * tan(δ) / L

			因此:
			下一时刻的车头朝向 = θ + V * tan(δ) / L * dt
v	车辆瞬时线速度	v = v + a * dt	瞬时速度: 下一时刻的速度 = 当前时刻的速度 + 加速度 * 时间间隔

上表中我们用(x, y, θ, v)表示自行车模型, 并给出了基于当前时刻的状态计算下一时刻状态的公式.

实现

我们可以用Python实现上述模型, 并生成行车辅助线.

def tractor(front_steer_angle=0.0, current_phi=float(math.pi / 2), vehicle_length=15.4, wheelbase=7.7):
    """
    :param front_steer_angle: 前轮转角
    :param current_phi: 车头朝向: 向前, 车体坐标, 摄像头位置为原点
    :param vehicle_length: 超过一个车长(15.4)米时停止计算
    :param wheelbase: 轴距
    :return: 轨迹
    """
 
    current_x = current_y = 0.0
    delta_distance = 0.1  # 每0.1米计算一个点
 
    total_distance = 0
    (x, y, phi) = ([], [], [])  # (轨迹坐标, 车体朝向)
    # https://zhuanlan.zhihu.com/p/128101546
    while total_distance < vehicle_length:
        next_x = current_x + delta_distance * math.cos(current_phi)
        next_y = current_y + delta_distance * math.sin(current_phi)
        next_phi = current_phi + delta_distance / wheelbase * math.tan(front_steer_angle)
        x.append(next_x)
        y.append(next_y)
        phi.append(next_phi)
 
        current_x = next_x
        current_y = next_y
        current_phi = next_phi
        total_distance += delta_distance
 
    return [x, y, phi]

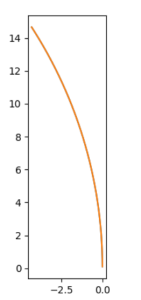
将轨迹拓展成辅助线

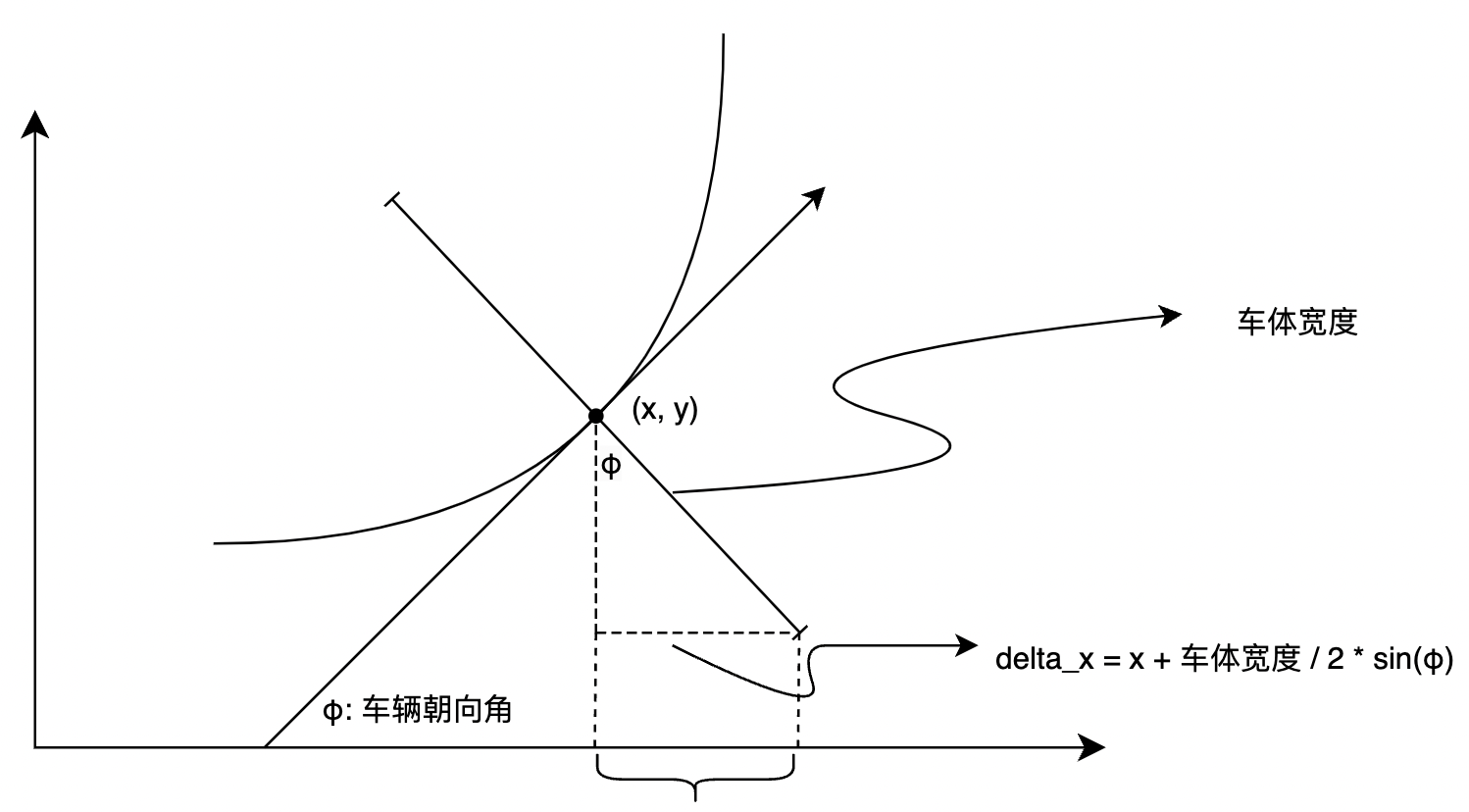
其中(x, y) 为任意轨迹点, delta_x为右侧车体对应点的x偏移量, 因此车辆右侧对应点的x坐标为: x_右 = x + delta_x. 相似的, 可以求的y_右, x_左, y_x, 不再赘述. 详情可见如下实现代码:

def trajectory2reference_line(x, y, phi, vehicle_width=2.85):
    # 根据轨迹拓展成左右两条线
    (left_x, left_y, right_x, right_y) = ([], [], [], [])
    for i in range(len(x)):
        base_x = x[i]
        base_y = y[i]
        base_phi = phi[i]
 
        left_x.append(base_x - vehicle_width / 2 * math.sin(base_phi))
        left_y.append(base_y + vehicle_width / 2 * math.cos(base_phi))
        right_x.append(base_x + vehicle_width / 2 * math.sin(base_phi))
        right_y.append(base_y - vehicle_width / 2 * math.cos(base_phi))
    return [left_x, left_y, right_x, right_y]

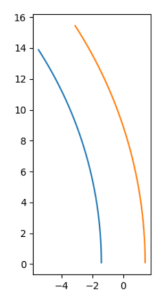
总结

本文介绍了自行车模型, 并实现了自行车模型的运动模型, 以及如何将车辆的轨迹拓展成行车辅助线. 本文的代码可以用于车辆运动的仿真, 以及车辆行驶的辅助线生成.

代码实现的是后轴中心的行车轨迹, 如果要实现前轴中心的行车轨迹, 需要对轨迹计算作业微调.